2. 佛山市南海百容水产良种有限公司, 广东 佛山 528216
2. Nanhai Bai-rong Aquatic Varieties Co. Ltd., Foshan 528216, China
草鱼(Ctenopharyngodon idellus)是中国重要的大宗淡水经济鱼类, 产量常年稳居养殖鱼类首位, 2016年达到589.88万t, 约占中国淡水鱼养殖总量的20%[1]。不过至今, 草鱼未有人工选育优良品种, 依赖良种促进产业增效增收的潜力还远未发掘。相反, 由于长期缺少定向选育计划, 加之有些苗种生产单位不注重亲本留种规程, 造成养殖群体抗逆性差、生长性能下降等种质退化问题日益突出, 制约着草鱼养殖业健康可持续发展。因此, 开发高产优质草鱼新品种成为产业发展亟需解决的重要课题。
在水产动物育种实践中, 选择育种是遗传改良最传统且行之有效的重要方法。该方法一般是在构建的基础选育种群之上, 针对目标性状进行累代选育[2]。对生长数量性状而言, 性状表型值受遗传和环境因素共同影响, 而且遗传效应中也只有加性效应部分(育种值)能够稳定遗传给后代。因此, 为了提升选择效率和精准度, 个体选留的评价指标应剔除固定环境效应, 剖离非加性遗传效应, 并准确估计育种值, 这成为数量性状选择育种的核心要素。不过, 育种值无法直接观测, 需要利用个体系谱和表型等信息建立统计分析模型, 并对混合模型方程组(mixed model equation, MME)进行求解, 包括对固定效应的估计和对随机遗传效应的预测[3]。在育种值估计方法中, 最佳线性无偏预测法(best linear unbiased prediction, BLUP)获得的个体育种值具有最佳线性无偏性和较高精确性, 目前应用广泛[4-5]。基于BLUP遗传评定为核心的育种体系在畜禽和水产动物选育中取得了显著的遗传进展[2, 6-7]。
遗传参数估计是育种值估计的前提条件, 也是了解目标性状遗传机制, 制定和优化选育路线的重要基础。从统计学上来讲, 遗传参数估计可归结为方差(协方差)组分的估计。对于常见的非均衡实验数据来说, 如何准确估计方差组分是育种学家所要追求的。随着计算机技术和育种理论的发展, 新的估计方法不断涌现, 其中, 约束极大似然法(REML)是目前动物育种遗传参数估计中较为理想的方法[3]。研究表明, 在样本量较大时, REML具有渐进无偏性和样本有效性, 估计遗传力更接近真值[8]。
综上所述, 准确估计遗传参数和育种值是实施选育计划的基础, 并直接影响动物选育目标性状的遗传进展和选育效果。因此, 本研究从草鱼生长性状选育核心种群中挑选亲本, 采用人工授精方式建立家系, 选用动物模型(线性混合模型), 利用ASReml软件中的REML和BLUP法对草鱼体重、体长、体高和肥满度性状进行遗传评定, 同时比较育种值选择和表型值选择差异, 为正在开展的快长草鱼新品种选育提供依据和技术支持。
1 材料和方法 1.1 家系的构建和培育本实验是在中国水产科学研究院珠江水产研究所佛山丹灶基地(佛山市南海百容水产良种有限公司)开展的。实验群体为草鱼生长性状选育核心种群, 是源于长江和珠江流域收集的不同地理群体[9]。每尾亲鱼均注射有PIT电子芯片标记, 池塘混养, 繁殖前强化培育。
从选育核心种群中随机挑选性腺发育良好, 体型健壮的亲鱼, 催产繁殖。采用人工授精方式成功地建立了21个全同胞草鱼家系, 其中包括4个母系半同胞家系和2个父系半同胞家系, 总计35尾亲鱼(16尾雌鱼, 19尾雄鱼)参与了家系构建工作。每个家系取适量受精卵, 放置在独立孵化桶内流水孵化, 全部家系1天内构建完成。
待仔鱼孵出3 d后, 每个家系随机取约3000尾水花, 转入室内水泥池精心培育。养至2~3 cm时, 每个家系随机取500尾转入户外分隔网箱内继续培育。培育过程中尽量保持各家系饲养密度和条件一致, 减少环境差异。待家系个体平均体重达到约30 g时, 从每个家系中随机取约150尾个体, 植入PIT电子芯片, 腹腔注射, 同时记录个体的芯片信息、父母本编号、家系编号等。标记工作3 d内完成, 标记后的个体全部放入一口5亩(1亩=666.66 m2)池塘混养。
1.2 性状测量当家系草鱼养至16月龄, 平均达到上市规格时, 测量收获生长性状观测值。为减轻测量操作对实验鱼的人为伤害, 先采用MS-222将捕获草鱼轻度麻醉, 再扫描鱼体内PIT电子芯片信息, 电子天平称鱼体重(body weight, BW), 同时用数码相机对目标鱼与标尺一同拍照留样。利用开发的鱼类外部形态测量软件(登记号: 2013SR144497)非接触式测量鱼体, 即通过采集图像的像素信息, 换算得到鱼体体长(standard length, SL)和体高(body height, BH)数据。根据获得的鱼体体长和体重数据, 计算肥满度(Fulton’s condition factor, K), 计算公式为:
建立线性模型, 通过ASReml-R软件估计草鱼各收获生长性状的方差组分; 采用软件中的约束极大似然法(REML)和最佳线性无偏预测法(BLUP)进行遗传参数和育种值估计。
| $ {Y_{ij}}{\rm{ = }}\mu + {a_i} + {f_j} + {e_{ij}} $ |
式中,
遗传力计算公式为:
| ${h^2} = \sigma _a/\sigma _{\text{P}}^2$ |
式中,
通过ASReml-R软件运用两性状动物模型估计表型相关系数(
| $ {r_{\rm{P}}} = \frac{{{\rm{CO}}{{\rm{V}}_{\rm{P}}}\left( {t1, t2} \right)}}{{{\sigma _{\rm{P}}}\left( {t1} \right){\sigma _{\rm{P}}}\left( {t2} \right)}}, {r_{\rm{s}}} = \frac{{{\rm{CO}}{{\rm{V}}_{\rm{s}}}\left( {t1, t2} \right)}}{{{\sigma _{\rm{s}}}\left( {t1} \right){\sigma _{\rm{s}}}\left( {t2} \right)}} $ |
式中, t1和t2分别为同一个体的2个性状表型值,
遗传变异系数计算公式为:
| ${\rm{GCV }}\left( \% \right) = \left( {{\sigma _{\rm{ \mathsf{ α} }}}/\bar x} \right) \times 100\% $ |
预期遗传进度计算公式为:
| $\Delta G = \theta \cdot{\sigma _{\rm{ \mathsf{ α} }}}\cdot\sqrt {{h^2}} $ |
相对遗传进度计算公式为:
| ${\rm{\Delta }}G'\left( \% \right) = \left( {\theta \cdot {\sigma _{\rm{ \mathsf{ α} }}} \cdot \sqrt {{h^2}} } \right) \times 100{\rm{\% }}/\bar x$ |
式中,
草鱼家系群体16月龄生长性状的描述性统计量见表 1, 各性状观测值经Kolmogorov-Smirnov检验均符合正态分布。在4个生长性状中, 体重性状的变异系数最高, 为27.98%;肥满度性状最低, 为7.32%;体长和体高的变异系数接近, 约为10%。其中, 体重最大个体比最小个体高出约4倍。
|
|
表 1 草鱼16月龄生长性状的描述性统计量 Tab.1 Descriptive statistics of growth traits of Ctenopharyngodon idella at 16 months age |
以箱线图形式给出21个草鱼全同胞家系收获体重(图 1a)、体长(图 1b)、体高(图 1c)和肥满度(图 1d)的上限阈值、上四分位数、中位数、下四分位数、下限阈值, 以及部分家系出现的异常值。图 1横坐标家系编号是以性状平均值大小进行排列, 从图中可见家系均值与中位数的排序格局基本一致。4个性状的家系均值变化范围为: 893.65~1749.99 g, 35.89~45.11 cm, 8.39~10.51 cm和1.80~2.09 g/cm3, 经一般线性模型分析表明, 家系间性状差异极显著(P < 0.01)。以体重性状为例, 排名首位的F16号家系平均体重(1749.99 g)比群体水平(1302.35 g)高出34.4%, 比最低位F20号家系(893.65 g)高出95.8%。以上数据表明, 草鱼选育核心种群的生长性状存在较大遗传变异和改良空间。
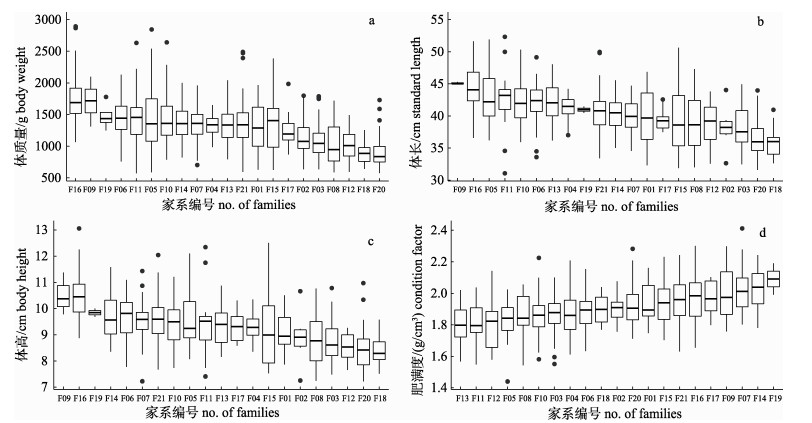
|
图 1 草鱼家系体重(a)、体长(b)、体高(c)和肥满度(d)性状箱线图
箱线图包含6个数据节点, 分别是上限(Q3+1.5 IQR), 上四分位数(Q3), 中位数, 下四分位数(Q1), 下限(Q1-1.5 IQR)和异常值, 其中异常值用“•”表示. Fig.1 Box plots of body weight (a), standard length (b), body height (c) and condition factor (d) for Ctenopharyngodon idellus families The box plots consist of upper limit (Q3+1.5 IQR), 75th percentile (Q3), median, 25th percentile (Q1), lower limit (Q1-1.5 IQR) and outliers, respectively. The outliers are shown with"•". |
应用单性状动物模型分析表型数据, 获得草鱼生长性状的方差组分、共同环境系数和遗传力估计值, 结果见表 2。收获体重、体长和体高性状的遗传力分别为0.39、0.47和0.21, 属中高遗传力; 肥满度性状为0.11, 属低遗传力(h2 < 0.2, 为低遗传力; 0.2≤h2≤0.4, 为中等遗传力; h2 > 0.4, 为高遗传力[10])。相较于加性遗传效应, 4个性状的共同环境系数范围为0.07~0.17, 共同环境效应值相近且影响不大。
|
|
表 2 利用动物模型估计的草鱼生长性状方差组分 Tab.2 Variance components estimation of growth traits in Ctenopharyngodon idellus using animal model |
应用两性状动物模型估计性状间的表型相关和遗传相关系数, 结果见表 3。4个性状间遗传相关与表型相关的格局基本一致。其中, 体重与体长的表型和遗传相关系数均是最高(r=0.95~0.97), 表现为高度正相关; 体高与体重也具有较高相关性(r=0.93~0.97), 与体长相关性稍小(r=0.88~0.89)。结果表明, 对体重、体长或体高进行单性状选育具有目标一致的特点。肥满度性状与其他3个性状间的相关性接近零(r=–0.15~0.19), 只与体高性状间有一定遗传正相关(r=0.43), 说明肥满度性状遗传上相对独立, 不过如对体高性状进行正向选择, 需考虑潜在引起鱼体肥满度增大的不利影响。此外, 综合各性状遗传变异系数和遗传进度(表 4)可知, 在一定选择强度下(10%留种率), 体重性状的选育潜力最大, 易于获得较大的遗传进展和选择效果。
|
|
表 3 草鱼生长性状表型相关(对角线下方)和遗传相关(对角线上方) Tab.3 Phenotypic correlation (below diagonal) and genetic correlation (above diagonal) for growth traits in Ctenopharyngodon idella |
|
|
表 4 草鱼生长性状的遗传变异系数与遗传进度 Tab.4 Genetic variation coefficients and genetic advances of growth traits in Ctenopharyngodon idellus |
通过ASReml-R软件提取个体育种值, 将个体各性状表型值和育种值进行Pearson相关性分析(表 5)。结果显示, 4个性状各自表型值与育种值之间相关系数范围为0.77~0.93, 统计检验均达到极显著水平(P < 0.01)。另外, 两性状育种值相关关系与前述遗传相关格局大体一致, 数值间的细微变化源于2种遗传算法的不同。
|
|
表 5 草鱼生长性状育种值与表型值的相关性分析 Tab.5 Correlation between breeding and phenotypic values of growth traits in Ctenopharyngodon idellus |
基于单性状表型值和育种值分别进行个体选择, 按10%留种率, 2种方法选择结果见表 6, 4个性状选留种用个体相同率分别为79.39%、81.82%、72.73%和68.75%;进一步比对发现, 基于单性状育种值选留个体的育种值秩次, 与其所对应的表型值秩次有较大差别, 秩相关系数分别为0.69、0.81、0.51和0.19。数据分析表明, 基于个体性状表型值或育种值进行选择, 2种选择结果存在差异, 而且当目标性状遗传力越低, 选择差异程度越大, 呈反比例关系。研究还发现, 基于育种值留种个体所涉及的家系数量均少于表型值选择。
|
|
表 6 基于表型值和育种值的个体选择比较(按10%留种率) Tab.6 Comparison of individual selection on phenotypic and breeding values under 10% selective pressure |
遗传变异是选择育种的基础。根据本研究草鱼生长数据的标准差、全距(极差)和箱形图来看, 4个性状的变异范围均较大, 而且同塘养殖环境下, 家系间表现出极显著差异, 说明选育核心种群具备较好的选择空间。其中, 体重性状的变异系数最高, 体长、体高性状次之, 肥满度性状较低, 这与虹鳟(Oncorhynchus mykiss)、尖吻鲈(Lates calcarifer)、欧洲鳎(Solea solea)等鱼类情况基本一致[12-14]。
遗传力是选择改良性状时的重要遗传参数, 是育种目标性状取舍、个体遗传评定的重要依据。Gjedrem等[15]汇总水产动物经济性状的遗传参数特征, 显示鱼类生长性状的遗传力总体处于中高等水平, 其中收获体重性状(11份遗传力数据)的均值为0.37。本研究获得的草鱼生长性状的遗传力(不含肥满度性状)为0.21~0.47, 与其他物种参数估计范围大体一致。同样, Fu等[16-17]对40日龄、10月龄和18月龄(均重846.6 g)的草鱼进行遗传参数评估, 也得出相似结果, 范围为0.24~0.38。在遗传参数评估中, 考虑到非加性遗传效应可能的影响, 本研究将全同胞家系效应(共同环境效应)加入到分析模型中, 发现共同环境效应值范围为0.07~0.17, 有别于Fu等[16]在草鱼研究中近乎为零的估计范围(0.00~0.06), 这很可能是源于本实验草鱼家系在同塘养殖前有较长时间的分池单养经历。不过综合来看, 共同环境效应, 包括母体效应, 对草鱼生长差异影响较小。另外, 本研究估计的性状遗传力标准误较大, 虽然尝试了其他几种统计模型, 但拟合效果并不理想, 这可能与数据结构、交配策略等因素有关[18-19]。例如, 实验所用F1家系亲本为随机挑选配对, 系谱矩阵是在假设亲本间无亲缘关系的基础上生成的, 实际情况或许存在偏差。其次, 构建的系谱结构较简单, 家系数量不多, 也会引起标准误增加[20]。
在鱼类形态学选育指标中, 肥满度性状常被用于反映鱼体的肥度、体型状况, 其中Fulton’s K肥满度, 即K=(体重/体长3)使用最为广泛。本研究估计的草鱼肥满度性状遗传力较低(h2=0.11), Fu等[17]观测草鱼幼鱼阶段的肥满度性状也有类似结果(h2=0.15)。不同于体重、体长等直接度量性状, 肥满度性状是通过经验公式换算得来。Fulton’s K是假定动物期望体重随着体长增长均匀增加[21], 而实际草鱼家系间和家系内个体生长速度各异, 推测一定程度上影响了评价指标的准确性[22]。此外, 鱼类肥满度性状的遗传力大小也显示出种属差异。例如, 鲤(Cyprinus carpio)和多种鲑科鱼类评估普遍较高[23-24], 罗非鱼(Oreochromis niloticus)、金头鲷(Sparus auratus)、尖吻鲈等则较低[25-27]。
3.2 目标性状的选择生物作为一个有机整体, 由于基因的一因多效和基因间连锁不平衡, 使得各性状之间存在内在关联[11]。在数量遗传学上, 通常采用遗传相关系数来描述不同性状间由遗传原因造成的相关程度大小, 这也成为间接选择、早期选种等育种策略制定的重要依据[28]。本研究中, 体重、体长和体高性状之间的表型和遗传相关均为高度正相关(r=0.88~0.97), 表明对其中某一性状进行选择, 其他2个性状也能相应得到改良, 这将简化选育过程中筛选操作的工作量。不过对体高性状而言, 考虑到肥满度性状与其存在遗传正相关(r=0.43), 以及草鱼修长的体型更符合大众消费者喜好, 所以应谨慎将其作为目标性状。除此之外, 结合对遗传变异系数和遗传进度数据的进一步分析, 体长性状的遗传力虽然高于体重性状, 但其变异幅度和相对遗传进度均较小, 加之育种实践中体重相比体长测量的便捷性, 因此以体重为目标的单性状选择可以更加有效地改良草鱼的生长性能。当然, 以上结论是在暂不考虑草鱼其他重要经济性状且未知遗传相关情况下得出的。
3.3 选择方法的比较相较于传统的表型选择, 动物模型BLUP法充分利用亲属信息, 理论上对个体育种值有着更为准确的估计, 从而提高遗传进展。本研究采用BLUP法估计个体育种值, 比较了育种值选择与表型值选择的差异。在本实例中, 从估算的性状育种值与表型值相关性分析来看, 二者整体差异并不明显。当按照10%留种率, 基于个体性状育种值和表型值分别进行择优筛选, 2种方法所选择个体的相同率出现偏差, 尤其选中个体的秩次排序有较大波动, 同时表现出目标性状遗传力越小, 选择差异越大的反比例关系。这说明, 对于低遗传力性状, 由于表型值受外界环境因素的影响大, 必然引起个体表型值与育种值间出现较大偏差, 间接支持了动物模型BULP法对低遗传力性状选育更有效的观点[29-30]。例如, Belonsky等[31]通过模拟猪闭锁核心群进行单性状选择发现, BULP法要好于简单的表型选择效果, 但如果随着目标选育性状遗传力从0.1增至0.6, 相对选择优势则从55%下降至10%。
统计2种选择方法保留家系的情况发现, 基于育种值留种个体, 所涉及保留的家系数量要少于表型值选择, 不过这些家系均包含在基于表型值保留家系的范围内。换言之, 个体所在家系的表现显著影响个体本身种用价值的估计, 使得BLUP法选取的个体往往聚焦在少数优良家系, 以达到选择进展的最大化, 由此也可能引起选育群体近交水平增速过快的不利影响[32-33]。例如, Gallardo等[34]通过BLUP法改良银大麻哈鱼收获体重性状, 当选育至F4代时, 选育基础种群中56%~76%的亲本没有贡献后代, 近交水平也显著增加。因此, 采用BLUP评价选育体系时, 需要制订更为合理的交配方案, 以控制近交系数的大幅攀升[35]。
综上所述, 本研究采用人工授精方式构建21个草鱼全同胞家系, 并选用动物模型对16月龄草鱼生长性状进行遗传参数和育种值估计。研究表明, 草鱼选育种群生长性状存在丰富变异, 而且以体重为目标性状可便捷、有效的改良草鱼生长性能。在选留种用个体时, 以BLUP遗传评定为基础的方法, 可显著增加预期遗传进展, 但也带来近交水平提升较快的风险。本研究可为草鱼生长性状选择育种提供理论依据和技术支撑。
致谢: 感谢在论文数据分析过程中, ASReml QQ交流群里的林元震、刘宝锁、栾生等老师以及多位同仁给予的支持和帮助。| [1] |
Bureau of Fisheries, Ministry of Agriculture. China Fishery Statistical Yearbook[M]. Beijing: China Agriculture Press, 2017. [农业部渔业渔政管理局. 中国渔业统计年鉴[M]. 北京: 中国农业出版社, 2017.]
|
| [2] |
Wang Q Y. Principles and Practices of Breeding in Aquatic Organisms[M]. Beijing: Science Press, 2013. [王清印. 水产生物育种理论与实践[M]. 北京: 科学出版社, 2013.]
|
| [3] |
Zhang Q. Calculation Methods for Animal Genetic and Breeding[M]. Beijing: Science Press, 2007. [张勤. 动物遗传育种中的计算方法[M]. 北京: 科学出版社, 2007.]
|
| [4] |
Mrode R A. Linear Models for the Prediction of Animal Breeding Values[J]. CABI Publishing, 2014. |
| [5] |
Zhai H Q, Wang J K. Applied Quantitative Genetics[M]. Beijing: China Agricultural Science and Technology Press, 2007. [翟虎渠, 王建康. 应用数量遗传[M]. 北京: 中国农业科学技术出版社, 2007.]
|
| [6] |
Schneeberger M, Barwick S A, Crow G H, et al. Economic indices using breeding values predicted by BLUP[J]. Journal of Animal Breeding and Genetics, 1992, 109(1-6): 180-187. DOI:10.1111/jbg.1992.109.issue-1-6 |
| [7] |
Ponzoni R W, Hamzah A, Tan S, et al. Genetic parameters and response to selection for live weight in the GIFT strain of Nile Tilapia (Oreochromis niloticus)[J]. Aquaculture, 2005, 247(1): 203-210. |
| [8] |
Gilmour A R, Thompson R, Cullis B R. Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models[J]. Biometrics, 1995, 51(4): 1440-1450. DOI:10.2307/2533274 |
| [9] |
Fan J, Chen B, Bai J, et al. Growth performance of hybrid progenies of grass carp (Ctenopharyngodon idella) populations from different geographical origins[J]. Agricultural Science & Technology, 2016, 17(2): 349-352, 475. |
| [10] |
Lou Y D. Fish Breeding[M]. Beijing: China Agriculture Press, 2001. [楼允东. 鱼类育种学[M]. 北京: 中国农业出版社, 2001.]
|
| [11] |
Sheng Z, Chen Y. Quantitative Genetics[M]. Beijing: Science Press, 1999: 164-173. [盛志廉, 陈瑶生. 数量遗传学[M]. 北京: 科学出版社, 1999: 164-173.]
|
| [12] |
Fishback A G, Danzmann R G, Ferguson M M, et al. Estimates of genetic parameters and genotype by environment interactions for growth traits of rainbow trout (Oncorhynchus mykiss) as inferred using molecular pedigrees[J]. Aquaculture, 2002, 206(3): 137-150. |
| [13] |
Wang C M, Lo L C, Zhu Z Y, et al. Estimating reproductive success of brooders and heritability of growth traits in Asian sea bass (Lates calcarifer) using microsatellites[J]. Aquac Res, 2008, 39(15): 1612-1619. |
| [14] |
Blonk R J W, Komen J, Tenghe A, et al. Heritability of shape in common sole, Solea solea, estimated from image analysis data[J]. Aquaculture, 2010, 307(1-2): 6-11. DOI:10.1016/j.aquaculture.2010.06.025 |
| [15] |
Gjedrem T, Robinson N. Advances by selective breeding for aquatic species: a review[J]. Agricultural Sciences, 2014, 5(12): 1152-1158. DOI:10.4236/as.2014.512125 |
| [16] |
Fu J, Shen Y, Xu X, et al. Genetic parameter estimates for growth of grass carp, Ctenopharyngodon idella, at 10 and 18 months of age[J]. Aquaculture, 2016, 450: 342-348. DOI:10.1016/j.aquaculture.2015.08.018 |
| [17] |
Fu J, Shen Y, Xu X, et al. Genetic parameter estimates and genotype by environment interaction analyses for early growth traits in grass carp (Ctenopharyngodon idella)[J]. Aquaculture International, 2015, 23(6): 1427-1441. DOI:10.1007/s10499-015-9894-7 |
| [18] |
Milner J M, Pemberton J M, Brotherstone S, et al. Estimating variance components and heritabilities in the wild: A case study using the 'animal model' approach[J]. Journal of Evolutionary Biology, 2000, 13: 804-813. DOI:10.1046/j.1420-9101.2000.00222.x |
| [19] |
Pérez-Rostro C I, Ibarra A M. Quantitative genetic parameter estimates for size and growth rate traits in Pacific white shrimp, Penaeus vannamei (Boone 1931) when reared indoors[J]. Aquaculture Research, 2003, 34(7): 543-553. DOI:10.1046/j.1365-2109.2003.00851.x |
| [20] |
Barrey E, Valette J P, Jouglin M, et al. Heritability of percentage of fast myosin heavy chains in skeletal muscles and relationship with performance[J]. Equine Veterinary Journal, 1999, 31(S30): 289-292. |
| [21] |
Dai Q, Dai J H, Li C, et al. Discussion on relative fatness[J]. Chinese Journal of Applied and Environmental Biology, 2006, 12: 715-718. [戴强, 戴建洪, 李成, 等. 关于肥满度指数的讨论[J]. 应用与环境生物学报, 2006, 12: 715-718. DOI:10.3321/j.issn:1006-687X.2006.05.026] |
| [22] |
Richter H, Lückst dt C, Focken U L, et al. An improved procedure to assess fish condition on the basis of length-weight relationships[J]. Archive of Fishery and Marine Research, 2000, 48: 255-264. |
| [23] |
Vandeputte M, Kocour M, Mauger S, et al. Heritability estimates for growth-related traits using microsatellite parentage assignment in juvenile common carp (Cyprinus carpio L.)[J]. Aquaculture, 2004, 235(1-4): 223-236. DOI:10.1016/j.aquaculture.2003.12.019 |
| [24] |
Carlson S M, Seamons T R. A review of quantitative genetic components of fitness in salmonids: implications for adaptation to future change[J]. Evolutionary Applications, 2008, 1(2): 222-238. DOI:10.1111/j.1752-4571.2008.00025.x |
| [25] |
Trọng T Q, Mulder H A, van Arendonk J A M, et al. Heritability and genotype by environment interaction estimates for harvest weight, growth rate, and shape of Nile tilapia (Oreochromis niloticus) grown in river cage and VAC in Vietnam[J]. Aquaculture, 2013, 384: 119-127. |
| [26] |
Navarro A, Zamorano M J, Hildebrandt S, et al. Estimates of heritabilities and genetic correlations for growth and carcass traits in gilthead seabream (Sparus auratus L.), under industrial conditions[J]. Aquaculture, 2009, 289(3-4): 225-230. DOI:10.1016/j.aquaculture.2008.12.024 |
| [27] |
Domingos J A, Smith-Keune C, Robinson N, et al. Heritability of harvest growth traits and genotype-environment interactions in barramundi, Lates calcarifer (Bloch)[J]. Aquaculture, 2013, 402: 66-75. |
| [28] |
Wang J Y, Chen G H. Quantitative Genetics and Animal Breeding[M]. Nanjing: Southeast University Press, 2004. [王金玉, 陈国宏. 数量遗传与动物育种[M]. 南京: 东南大学出版社, 2004.]
|
| [29] |
Morris A J, Pollott G E. Comparison of selection based on phenotype, selection index and best linear unbiased prediction using data from a closed broiler line[J]. British Poultry Science, 1997, 38(3): 249-254. DOI:10.1080/00071669708417981 |
| [30] |
Sun S Y. Summarization of animal model BLUP and its application[J]. Journal of Veterinary Medical Science, 2008, 27: 56-59, 62. [孙寿永. 动物模型BLUP法及其应用的综述[J]. 畜牧兽医杂志, 2008, 27: 56-59, 62.] |
| [31] |
Belonsky G M, Kennedy B W. Selection on individual phenotype and best linear unbiased predictor of breeding value in a closed swine herd[J]. Journal of Animal Science, 1988, 66(5): 1124-1131. DOI:10.2527/jas1988.6651124x |
| [32] |
Quinton M, Smith C, Goddard M E. Comparison of selection methods at the same level of inbreeding[J]. Journal of Animal Science, 1992, 70(4): 1060-1067. DOI:10.2527/1992.7041060x |
| [33] |
Luan S, Kong J, Wang Q Y. Methods and application of aquatic animal breeding value estimation: A review[J]. Marine Fisheries Research, 2008, 29: 101-107. [栾生, 孔杰, 王清印. 水产动物育种值估计方法及其应用的研究进展[J]. 渔业科学进展, 2008, 29: 101-107.] |
| [34] |
Gallardo J A, Garcı́a X, Lhorente J P, et al. Inbreeding and inbreeding depression of female reproductive traits in two populations of Coho salmon selected using BLUP predictors of breeding values[J]. Aquaculture, 2004, 234(1): 111-122. |
| [35] |
Quinton M, Smith C. Comparison of evaluation-selection systems for maximizing genetic response at the same level of inbreeding[J]. Journal of Animal Science, 1995, 73(8): 2208-2212. DOI:10.2527/1995.7382208x |
 2018, Vol. 25
2018, Vol. 25

