2. 大洋渔业资源可持续开发省部共建教育部重点实验室, 上海 201306
2. The Key Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China
印度洋黄鳍金枪鱼(Thunnus albacares)主要分布于阿拉伯海、非洲东部沿海及外海、孟加拉湾及印度尼西亚群岛西部海域[1], 被工业型渔业(industrial fisheries)与生计型渔业(artisanal fisheries)所利用, 近年, 两者各约占50%[2]。工业型渔业主要有法国、西班牙的围网渔业, 印度尼西亚、中国台湾的冰鲜延绳钓渔业, 以及日本、中国台湾、韩国的超低温延绳钓渔业。生计型渔业主要包括马尔代夫、印度等国的手钓、竿钓渔业, 伊朗、斯里兰卡等国的刺网渔业等[2]。随捕捞强度的增大, 印度洋黄鳍金枪鱼的资源状况越来越受到国际组织的关注[1]。我国学者从食性[3]、渔场及其与海洋环境的关系[4-5]、资源评估[1]等方面对印度洋黄鳍金枪鱼进行了深入研究。
印度洋黄鳍金枪鱼渔业数据的收集始于1950年, 但数据存在一定的质量问题, 如体长组成数据存在缺失、样本数较小或采样方法变化等问题[2, 6]。印度洋黄鳍金枪鱼资源丰度指数数据主要为日本和中国台湾延绳钓渔业的标准化单位捕捞努力渔获量(catch per unit effort, CPUE)数据, 这些数据也受捕捞位置及目标鱼种变化等因素的影响而存在较大的不确定性[2]。
尽管资源合成(Stock Synthesis version 3, SS3)模型[7]用于确定当前印度洋黄鳍金枪鱼的资源状态, 但受渔业数据质量、关键参数设置缺少可靠研究支持等因素的影响, 其评估结果仍受到质疑[2]。
由于不同评估模型的假设及数据需求各不相同, 而模型的评估效果往往取决于模型所需的假设及数据被满足的程度[8]。因此, 采用多种模型对印度洋黄鳍金枪鱼资源进行评估, 并比较多种模型的评估结果, 将使印度洋黄鳍金枪鱼的评估与管理更科学[1]。为此, 本研究尝试采用贝叶斯生物量动态模型(Bayesian biomass dynamic model, BBDM)[9]对印度洋黄鳍金枪鱼进行资源评估。选择生物量动态模型可避免使用有问题的年龄或体长组成数据, 减少不确定的参数或假设, 而采用贝叶斯方法估计参数, 则可利用先验信息降低参数估计的不确定性以提高资源评估结果的质量。本研究将丰富印度洋黄鳍金枪鱼的资源评估方法, 为印度洋黄鳍金枪鱼的科学管理提供参考依据。
1 材料与方法 1.1 渔获量与标准化CPUE数据渔获量与标准化CPUE数据来自印度洋金枪鱼委员会(Indian Ocean Tuna Commission, IOTC)网站(http://www.iotc.org/meetings/17th-working-party-tropical-tunas-wptt17)。渔获量数据时间跨度为1950—2014年。标准化CPUE数据分别来自日本延绳钓渔业[10]与中国台湾延绳钓渔业[11]。中国台湾延绳钓渔业的标准化CPUE数据时间跨度为1980—2012年。尽管日本延绳钓渔业的标准化CPUE数据时间跨度为1963—2014年, 但由于1963—1971年的CPUE大幅高于20世纪70年代后期的CPUE, 而20世纪80年代以前渔获量均较低, 因此认为1963—1971年的CPUE不能反映实际情况, 因此该时段的CPUE被舍弃[6]。
为更好设置先验分布并提高计算稳定性, 对渔获量与标准化CPUE数据进行归一化处理, 即:
| ${{Y}_{t}}=\frac{{{C}_{t}}}{{{C}_{\text{Max}}}}$ | (1) |
| ${{I}_{t}}=\frac{CPU{{E}_{t}}}{CPU{{E}_{\text{Max}}}}$ | (2) |
式中, Ct为t年的渔获量, CMax为最大渔获量, Yt为归一化产量, CPUEt为t年的标准化CPUE, CPUEMax为最大标准化CPUE, It为归一化资源指数。
1.2 生物量动态模型Fox形式的生物量动态模型如下[9]:
| ${{B}_{t+\vartriangle t}}={{e}^{\left\{ P-{{e}^{-r\vartriangle t}}[\mathit{P-r}\text{ln}\left( {{B}_{t}} \right)] \right\}/r}}$ | (3) |
| $P=r\ln \left( K \right)-{{F}_{t}}$ | (4) |
| ${{F}_{t}}=\frac{{{Y}_{t}}}{{{B}_{t}}}$ | (5) |
| ${{{\bar{B}}}_{t}}=\int_{0}^{\vartriangle t}{{{B}_{t+x}}\text{d}x}$ | (6) |
式中, r为内禀增长率, K为环境容纳量, Ft为t年的捕捞死亡系数, Bt为t年的生物量, Bt+Δt为t+Δt年的生物量, Δt通常设为1, 即1年, Yt为t年的渔获量。若已知r, K, Yt及起始年(即1950年)生物量(Bs), 则Ft与Bt可通过式(3)~式(6)迭代算出。
为估计参数, 假设归一化资源指数(It)与无法直接观察的状态变量Bt具有如下关系:
| ${{I}_{t}}|q,{{{\bar{B}}}_{t}},\tau =q{{{\bar{B}}}_{t}}{{e}^{{{\varepsilon }_{t}}}}$ | (7) |
式中, q为捕捞系数, εt为均值为0, 精度(precision)为τ(即方差的倒数)的正态分布随机变量, Y|X表示在给定X下Y的条件分布。
为提高参数估计质量, 对起始年生物量(Bs)重新参数化, 即:
| ${{B}_{s}}={{B}_{0}}K$ | (8) |
式中, B0为起始年生物量与环境容纳量的比值, 该值小于1, 大于0。
当采用Fox形式的生物量动态模型时, 最大可持续产量(maximum sustainable yield, MSY)及最大可持续产量下的捕捞死亡系数(FMSY)与生物量(BMSY)可由式(9)、(10)及(11)计算:
| $\text{MSY=}\frac{rK}{\rm{e}}$ | (9) |
| ${{F}_{\text{MSY}}}=r$ | (10) |
| ${{B}_{\text{MSY}}}=\frac{K}{\rm{e}}$ | (11) |
式中, e为自然常数, r为内禀增长率, K为环境容纳量。
若当前捕捞死亡系数大于FMSY时, 则出现捕捞型过度捕捞(overfishing), 而当前资源量小于BMSY时, 则出现资源型过度捕捞(overfished)。
1.3 参数先验设置 1.3.1 q、τ与K的先验设置q、τ与K均采用无信息先验。由式(1)与式(2)可知, q应小于1、大于0, 因此, 假设日本与中国台湾延绳钓渔业分别对应的捕捞系数(分别记作qJ与qT)均服从0~1的均匀分布, 记为U[0, 1]。假设日本与中国台湾延绳钓渔业标准化CPUE的精度(分别记作τJ与τT)均服从无信息的伽马分布, 其形状参数为0.001, 尺度参数的倒数为0.001, 记为G(0.001, 0.001)。根据多年资源评估结果[6, 12-14], 为足以覆盖K的合理范围, 本研究假设K的最小值为最大渔获量(5.29×105 t)的2倍(即1.06×106 t), 最大值为最大渔获量的32倍(即1.69×107 t)。因此, 假设被最大渔获量归一化后的K(记作K*)服从2~32的均匀分布, 记为U[2, 32]。
1.3.2 B0的先验设置由于B0应小于1.0, 同时由于1950年以前, 捕捞量极小, 因此, 1950年的生物量应该比较接近K, 为足以覆盖B0值的合理范围, 本研究假设B0的最小值为0.1。因此, 假设B0服从0.1~1.0的无信息均匀分布, 记为U[0.1, 1.0]。
1.3.3 r的先验设置r的先验设置分3种情况: (1)使用无信息均匀分布, 即假设r服从0.05~1.5的均匀分布, 记作U[0.05, 1.5]; (2)根据Carruthers等[15]的结果, 假设r服从中值与变异系数分别为0.48与0.20的对数正态分布, 记为LM (0.48, 0.20); (3)假设r服从对数正态分布, 记为LM, 其中值与变异系数, 利用种群统计学方法(demographic method)[16-17]求取。
利用种群统计学方法求取r的相关方程及步骤可参见文献[9], 方程中的相关参数设置如下:最大年龄设为15, 体重与体长关系中的生长条件因子(c)与幂指数系数(b)分别设为1.89×10-5与3.0195[13]; 由于黄鳍金枪鱼的陡度(h)取值一般为0.7、0.8及0.9[6], 因此假设h服从beta分布, 其均值为0.8, 标准差为0.05, 性成熟概率[14]、自然死亡系数[6]、每一年龄下的平均体长及其标准差[18]见表 1。
|
|
表 1 性成熟概率、自然死亡系数与平均体长及其标准差的取值 Tab.1 Values of parameters for maturity probability, natural mortality, mean length and standard deviation of length |
根据标准化CPUE数据、参数先验设置的不同, 可得9个评估模型, 分别记为S1~S9, 见表 2。
|
|
表 2 计算模型及其参数的先验设置 Tab.2 Prior of parameters for models |
基于贝叶斯方法的参数估计采用WinBUGS 14[19]软件实现, 具体代码参见文献[20], 模型收敛诊断采用Gelman-Rubin统计量, 并以1.1为阈值[21]。
若参数后验分布估计合理, 则当CPUE数据相同时, 采用偏差信息准则(deviance information criterion, DIC)[22]选择模型, 当CPUE数据不同时, 本研究将比较均方误差(mean square error, MSE)。
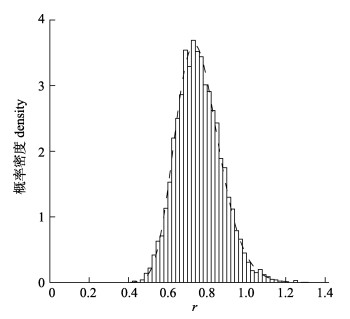
2 结果与分析 2.1 内禀增长率先验分布的估计采用种群统计学方法估计的内禀增长率r的先验分布与中值为0.75、变异系数为0.15的对数正态分布非常吻合(图 1)。该值和Carruthers等[15]的结果差异较大。
|
图 1 采用种群统计学方法估计的内禀增长率r的先验分布 虚线是中值为0.75、变异系数为0.15的对数正态分布. Fig.1 The prior distribution of intrinsic growth rate r estimated by using demographic methods The black dashed line is lognormal distribution with median and coefficient of variance assumed to be 0.75 and 0.15 respectively. |
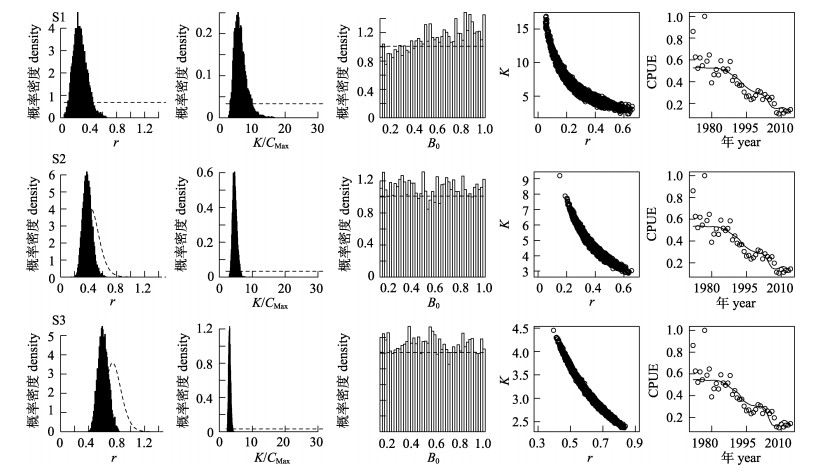
依Gelman-Rubin统计量, 所有模型均收敛。当使用日本标准化CPUE数据时(模型S1-S3), 除少数年份外, 所有模型均能较好拟合该CPUE数据, MSE约为0.01(图 2、表 3)。若r采用无信息先验分布, r与K的后验分布具有较大方差, B0的后验分布概率随B0值的增大而有增大趋势(图 2)。若r采用信息先验分布(即模型S2与S3), 尽管r的后验分布与先验分布存在较大差异, 但r的先验信息对参数估计影响明显, r与K的后验分布区间明显变窄, 方差有较大减少(图 2、表 3); 同时, B0的后验分布接近均匀分布(图 2); 相对于无信息先验模型(即模型S1), r后验分布中值随其先验中值的增大而增大, 而K后验分布中值则相应减少(表 3)。所有模型估计的r与K均呈显著的负相关关系(图 2)。3个模型均表明印度洋黄鳍金枪鱼被过度捕捞, 即既存在捕捞型过度捕捞, 也存在资源型过度捕捞, 且随r先验中值的增大, 过度捕捞程度有所减弱(表 3)。
|
图 2 模型S1、S2与S3的拟合结果
虚线为先验分布; 实线为预测的标准化CPUE, 散点为观测的标准化CPUE; r为内禀增长率, K为环境容纳量; CMax为最大渔获量; B0为起始年生物量与环境容纳量的比值.
Fig.2 The results estimated by using model S1, S2 and S3
The dashed line is the prior distribution of the parameters, the solid line is the predicted standardized CPUE and the points are the observed standardized CPUE; r is intrinsic rate of increase and K is carrying capacity; CMax is the maximum catch; B0 is the ratio of biomass in the first year to carrying capacity. |
|
|
表 3 各模型估计的结果 Tab.3 The results estimated or computed based on the models listed in table 2 |
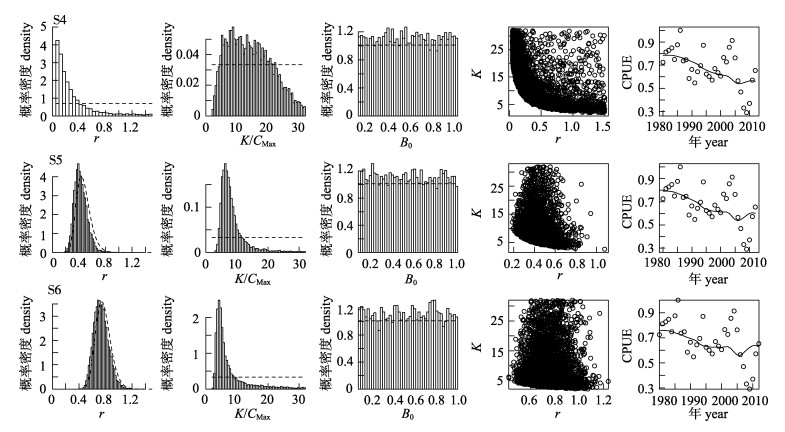
当使用中国台湾标准化CPUE数据时(模型S4~S6), 模型预测的CPUE与该标准化CPUE差异较大(图 3), MSE约为0.02(表 3)。若r采用无信息先验, r与K的后验分布具有明显的长尾, r与K仍呈显著的负相关关系(P < 0.05)。若r采用信息先验分布(模型S5-S6), r的后验分布与先验分布差异较小(图 3), K的后验分布仍具有明显的长尾, r与K的负相关关系进一步减弱(图 3)。相对于无信息先验模型(即S4), r后验分布中值随其先验分布中值的增大而增大, 而K后验分布中值则相应减少(表 3)。所有模型估计的B0的后验分布均接近均匀分布(图 3)。模型S4、S5及S6的评估结果均较乐观, 3个模型的结果均表明印度洋黄鳍金枪鱼没有被过度捕捞, 并且随r先验中值的增大, 资源状况更加健康(表 3)。
|
图 3 模型S4、S5与S6的拟合结果 虚线为先验分布; 实线为预测的标准化CPUE, 散点为观测的标准化CPUE.r为内禀增长率, K为环境容纳量; CMax为最大渔获量; B0为起始年生物量与环境容纳量的比值. Fig.3 The results estimated by using model S4, S5 and S6 The dashed line is the prior distribution of the parameters; the solid line is the predicted standardized CPUE and the points are the observed standardized CPUE; r is intrinsic rate of increase and K is carrying capacity; CMax is the maximum catch; B0 is the ratio of biomass in the first year to carrying capacity. |
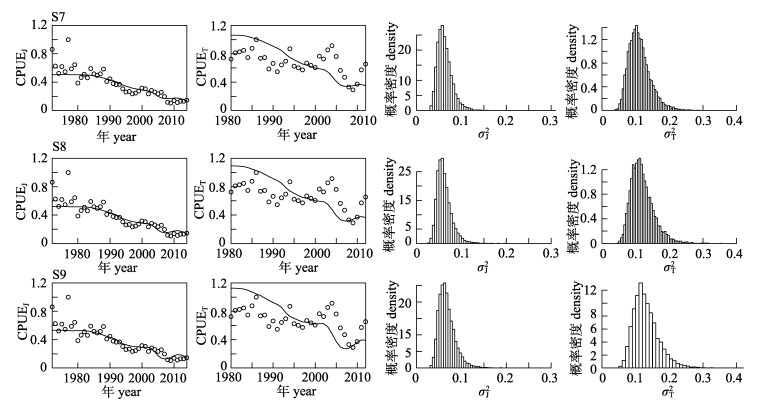
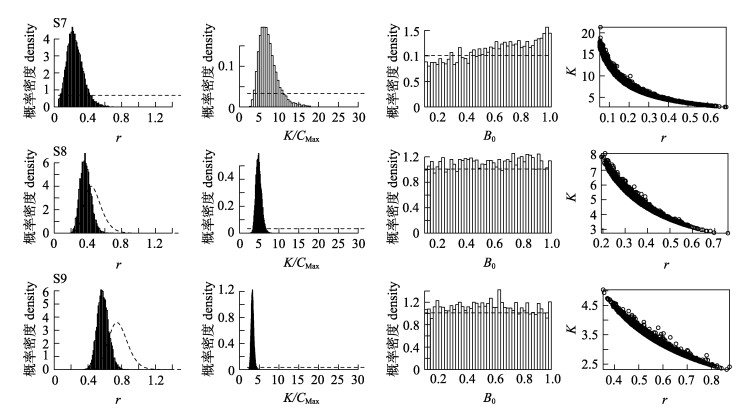
当同时使用日本与中国台湾标准化CPUE数据时(模型S7~S9), 所有模型均能较好拟合日本标准化CPUE数据, 但对中国台湾标准化CPUE数据的拟合较差(图 4), 拟合日本标准化CPUE的MSE约为0.01, 而拟合中国台湾标准化CPUE的MSE约为0.05(表 3)。日本标准化CPUE数据对应的方差明显小于中国台湾标准化CPUE数据所对应的方差(图 4), 这说明, 日本标准化CPUE数据在参数估计中具有更大的权重, 因此, 模型S7、S8与S9的参数估计结果也分别与模型S1、S2及S3类似(图 1、图 5、表 3)。
|
图 4 观测与模型S7, S8和S9预测的标准化CPUE及其方差的后验分布
实线为预测的标准化CPUE, 散点为观测的标准化CPUE; CPUEJ表示日本的标准化CPUE, CPUET表示中国台湾的标准化CPUE; σJ2为日本标准化CPUE的方差, 其值等于1/τJ, σT2为中国台湾标准化CPUE的方差, 其值等于1/τT.
Fig.4 The observed and predicted standardized CPUEs and the posterior distributions of their variance estimated by model S7, S8 and S9
The solid line is the predicted standardized CPUE and the points are the observed standardized CPUE; the CPUEJ and CPUET indicates the standardized CPUE from Japan and Taiwan, China respectively; σJ2which equals 1/τJ is variance of standardized CPUE of Japan and σT2 which equals 1/τT is variance of the standardized CPUE of Taiwan, China. |
|
图 5 模型S7、S8与S9估计的参数的后验分布及r与K的关系 虚线为先验分布; r为内禀增长率, K为环境容纳量; CMax为最大渔获量; B0为起始年生物量与环境容纳量的比值. Fig.5 The posterior distributions of the parameters and the relationship between r and K estimated by model S7, S8 and S9 The dashed line is the prior distribution of the parameters; r is intrinsic rate of increase and K is carrying capacity; CMax is the maximum catch; B0 is the ratio of biomass in the first year to carrying capacity. |
从对标准化CPUE拟合的结果看, 模型S1、S2、S3及模型S7、S8与S9明显好于模型S4、S5与S6(图 2、3、4与表 3)。模型S1的DIC最小, S2其次, 而S3最大, 同样, 模型S7的DIC最小, S8其次, 而S9最大(表 3)。由于模型S1与模型S7的B0的后验分布概率随B0值增大而增大(图 2与图 5), 这预示着B0具有大于1.0的趋势, 因此, 估计不合理。而就模型S2与S8而言, 两个模型拟合日本标准化CPUE的效果类似(MSE相等, 见表 3), 但模型S8同时利用了两个标准化CPUE的信息, 因此本研究选择模型S8用于确定印度洋黄鳍金枪鱼的资源状态。从模型S8的评估结果可知, r的中值为0.38, K的中值为2.55×106 t, MSY为3.45×105 t, 印度洋黄鳍金枪鱼资源既存在捕捞型过度捕捞, 也存在资源型过度捕捞。
3 讨论 3.1 生物量动态模型生物量动态模型对种群的补充、生长、死亡等过程进行了高度综合, 模型具有参数少、所需数据相对简单的特点。但生物量动态模型不能有效利用年龄或体长组成等信息, 难于更真实地模拟种群生物过程(如补充、生长、自然死亡)、渔业捕捞过程(如渔具选择性)对种群演化动态及管理参数计算的影响, 其结果常受到质疑[23-24]。
尽管年龄结构模型(如SS3)能利用更多信息, 但该类模型需要更多生物学与渔业数据的支持, 需估计更多参数, 且模型诊断更困难[8, 25]。由于印度洋黄鳍金枪鱼的种群结构、自然死亡系数、亲体与补充量关系等假设均缺少科学研究支持[6, 14], 年龄或体长组成数据因存在缺少样本、样本不具代表性或采样方案变化等问题而具有较大不确定性[2], 年龄结构模型的评估结果同样受到质疑[2]。
从研究结果看,生物量动态模型也能获得较好的评估效果[26]。由于生物量动态模型具有相对简单、所需数据容易收集等特点, 使基于生物量动态模型的资源评估软件, 如带协变量的产量模型(A Stock Production Model Incorporating Covariates, ASPIC)、贝叶斯剩余产量模型(Bayesian surplus production model, BSP)等仍被广泛应用于金枪鱼的资源评估中[27-28]。当参数采用无信息先验时,BSP与ASPIC的结果相似[27]。由于基于贝叶斯方法的生物量动态模型可有效利用已有的各种先验知识, 以约束参数估计, 使之处于合理的范围, 因而, 该类模型在数据有限或数据质量较差时较为有效[29]。
本研究没有采用Schaefer形式的生物量动态模型主要是因为其对称的产量曲线不太符合实际[30]。尽管一般生物量动态模型(generalized bio mass dynamic model)[30]通过增加一个形状参数从而使其可以更加灵活地拟合各种形状的产量曲线, 但形状参数较难准确估计, 因此, 一般生物量动态模型的应用仍有待进一步深入研究。
3.2 先验设置本研究主要采用均匀分布作为参数的无信息先验。均匀分布的上下边界如果设置不好, 如r与K的边界值, 会对其后验分布产生影响。为确定r与K的边界, 本研究参考了文献[15]、FishBase (http://www.fishbase.org/)及近年印度洋黄鳍金枪鱼资源评估结果[6, 12-14], 并考虑到这些结果可能存在的不确定性, 对边界区间进行了合理的放大。多组边界组合的试验结果表明, 本研究设置的r或K的边界值足以包含r与K取值的合理范围。
本研究估计的r的先验分布与Carruthers等[15]估计的结果存在较大差异, 从模型选择结果看, Carruthers等[11]估计的r的先验分布更为合理。Carruthers等[15]估计r先验分布的方法与本研究一致, 造成先验分布估计差异的原因是使用了不同生命史参数, 特别是自然死亡系数的差异较大。本研究使用的生命史参数与Langley[6]、Nishida等[14]在2015年印度洋黄鳍金枪鱼资源评估中使用的生命史参数基本一致。由于生命史参数中的陡度、自然死亡系数等对渔业资源评估结果具有非常重要的影响[6], 因此, 从本研究结果看, 这些生命史参数的选择可能存在问题, 这增加了这些评估模型评估结果的不确定性。
3.3 模型拟合分析 3.3.1 模型对CPUE的拟合由于中国台湾延绳钓渔业存在目标鱼种改变的现象, 如油鱼渔业(oilfish fishery)的发展, 使其捕捞系数产生很大的变化, 而CPUE标准化时很少考虑这些因素; 另一方面, 用于标准化CPUE的数据在1982—2000年期间对渔捞日志的覆盖率过低; 这些因素均影响了该渔业标准化CPUE的质量[2]。因此, Langley[6]、Nishida等[14]在印度洋黄鳍金枪鱼的资源评估中仅使用了日本延绳钓渔业的标准化CPUE数据。本研究结果也表明, 中国台湾标准化CPUE数据的有效信息有限(对r先验分布改变较小, 图 3), 模型拟合效果相对较差。尽管模型对日本标准化CPUE拟合较好, 但日本延绳钓渔业数据也存在捕捞努力量空间分布变化(如受索马里海盗影响引起相关海域捕捞努力量减少)、目标鱼种变化等问题而影响标准化CPUE的质量[2]。因此, 本研究认为通过估计两个标准化CPUE的方差以自动确定各CPUE在参数估计中的权重, 可利用两个CPUE的有效信息提高参数估计质量[29]。
3.3.2 先验设置对参数估计的影响生物量动态模型中的r与K存在较强的负相关关系[30], 同时, 由于印度洋黄鳍金枪鱼渔获量、资源指数数据均存在不确定性[2], 并且资源指数表现为经典的单调下降趋势(one-way trip), 更易使模型无法同时有效确定r与K的值[25, 30], 使r与K的后验分布形成长尾现象, 增加了r与K后验分布的方差。管理参数FMSY、BMSY, 直接由r与K计算, 因此, r与K估计的差异有可能导致对资源状态、资源恢复能力判断的差异[31], 从而影响管理策略的选择、管理措施的制定。对此种情形, 则需借助种群其他生物学信息, 以利用种群统计学等方法为r或K等参数提供先验信息, 方能提高生物量动态模型参数估计的可靠性[20, 27]。
当r采用无信息先验时, 所有模型估计的r的后验分布中值均小于0.27(表 3), 而据FishBase (http://www.fishbase.org/), 黄鳍金枪鱼的恢复力中等, r的95%置信区间范围在0.27 ~1.34之间。因此, 当r采用无信息先验时, 模型估计的r均偏小, 而K则相对偏大。当对r采用信息先验时, 有效地改善了所有参数的估计质量, 使r与K的后验分布处于相对合理的范围。
3.3.3 B0的估计B0的理论值大于0小于1, 但在使用生物量动态模型进行资源评估时, 该参数的估计值常大于1[32]。为此, 常采用惩罚函数以使其值限制在合理区间[32]或固定B0的值[28]。模型S1与S7估计的B0的后验分布具有明显单调上升趋势, 若将B0的分布区间从(0.1, 1.0)扩大至(0, 2.0), 其均值将会大于1[9], 因此, 本研究认为模型S1与S7估计的B0的后验分布不合理。
本研究使用的CPUE数据始于1972年, 因此, CPUE对1972年以前的资源量无法约束。同时, 在1950至1972年之间, 印度洋黄鳍金枪鱼的渔获量很低, 对于任何B0, 只要r与K不太小时, 资源均有足够时间进行恢复, 以满足对1972年及以后CPUE的合理拟合, 因此, B0后验分布接近均匀分布是合理的。在此情况下, 一般可固定B0为一常数(如0.90[28]), 并且对B0值的设置基本不会影响其他参数的估计。若r与K估计同时偏小时, 模型必须通过提高B0的值以达到一定的资源量来满足对CPUE的拟合, 从而使B0的估计不合理。
3.4 与其他评估模型结果的比较当前, IOTC采纳了SS3模型的评估结果[2, 6], 该结果表明, 印度洋黄鳍金枪鱼已被过度捕捞, 即资源型与捕捞型过度捕捞同时存在, 这与本研究结果一致。但本研究估计的MSY较低, 对资源状态的判断更悲观。由于两个模型的假设及结构差异很大, 所使用的数据非常不同, 如何正确评价两个模型的评估结果有待今后深入研究。
此外, 尽管本研究选择模型S8用于对资源状况的判断, 但由于模型使用的数据不同, 难于统一使用DIC等统计量选择模型, 而模型拟合CPUE的效果基本相似, DIC在模型选择中也存在不确定性[33], 因此, 本研究的模型选择具有不确定性。在渔业管理实践中, 应综合考虑模型S2、S3、S8及S9的结果。
致谢: 感谢印度洋金枪鱼委员会秘书处提供黄鳍金枪鱼资源评估所需的渔业和CPUE数据资料。| [1] |
Feng B, Chen X J, Nishida T. Stock assessment of Thunnus albacares in the Indian Ocean using age structure production model Ocean[J]. Acta Ecologica Sinica, 2010, 30(13): 3375-3384. [冯波, 陈新军, 西田勤. 应用年龄结构产量模型评估印度洋黄鳍金枪鱼资源[J]. 生态学报, 2010, 30(13): 3375-3384.] |
| [2] |
IOTC. Report of the 17th Session of the IOTC Working Party on Tropical Tunas (IOTC-2015-WPTT17-R[E])[R]. 17th Session of the IOTC Working Party on Tropical Tunas, Montpellier, France, 22-28 October 2015.
|
| [3] |
Zhu G P, Xu L X, Zhou Y Q, et al. Feeding habits and its seasonal variations of Thunnus albacores in the west-central Indian Ocean[J]. Journal of Fisheries of China, 2008, 32(5): 725-732. [朱国平, 许柳雄, 周应祺, 等. 印度洋中西部水域黄鳍金枪鱼的食性及其季节性变化[J]. 水产学报, 2008, 32(5): 725-732.] |
| [4] |
Yang S L, Zhang Y, Zhang H, et al. The relationship between the temporal-spatial distribution of fishing ground of yellowfin tuna (Thunnus albacares) and thermocline characteristics in the tropic Indian Ocean[J]. Acta Ecologica Sinica, 2012, 32(3): 671-679. [杨胜龙, 张禹, 张衡, 等. 热带印度洋黄鳍金枪鱼渔场时空分布与温跃层的关系[J]. 生态学报, 2012, 32(3): 671-679.] |
| [5] |
Yang X M, Dai X J, Zhu G P. Geostatistical analysis of spatial heterogeneity of yellowfin tuna (Thunnus albacares) purse seine catch in the western Indian Ocean[J]. Acta Ecologica Sinica, 2012, 32(15): 4682-4690. [杨晓明, 戴小杰, 朱国平. 基于地统计分析西印度洋黄鳍金枪鱼围网渔获量的空间异质性[J]. 生态学报, 2012, 32(15): 4682-4690.] |
| [6] |
Langley A. Stock assessment of yellowfin tuna in the Indian Ocean using Stock Synthesis (IOTC-2015-WPTT17-30)[R]. 17th Session of the IOTC Working Party on Tropical Tunas, Montpellier, France, 22-28 October 2015.
|
| [7] |
Methot R D, Wetzel C R. Stock synthesis: A biological and statistical framework for fish stock assessment and fishery management[J]. Fisheries Research, 2013, 142: 86-99. DOI:10.1016/j.fishres.2012.10.012 |
| [8] |
Guan W J, Tian S Q, Zhu J F, et al. A review of fisheries stock assessment models[J]. Journal of Fishery Sciences of China, 2013, 20(5): 1112-1120. [官文江, 田思泉, 朱江峰, 等. 渔业资源评估模型的研究现状与展望[J]. 中国水产科学, 2013, 20(5): 1112-1120.] |
| [9] |
Guan W J, Tang L, Zhu J F, et al. Application of a Bayesian method to data-poor stock assessment by using Indian Ocean albacore (Thunnus alalunga) stock assessment as an example[J]. Acta Oceanologica Sinica, 2016, 35(2): 117-125. DOI:10.1007/s13131-016-0814-0 |
| [10] |
Ochi D, Matsumoto T, Nishida T, et al. Update of standardized Japanese longline CPUE for yellowfin tuna in the Indian Ocean and consideration of standardization methods. (IOTC- 2015-WPTT17-26)[R]. 17th Session of the IOTC Working Party on Tropical Tunas, Montpellier, France, 22-28 October 2015.
|
| [11] |
Yeh Y M, Chang S T. CPUE standardizations for yellowfin tuna caught by Taiwan, China longline fishery in the Indian Ocean using generalized linear model (IOTC-2013- WPTT15-38)[R]. 15th Session of the IOTC Working Party on Tropical Tunas, San Sebastian, Spain, 23-28 October 2013.
|
| [12] |
Langley A, Herrera M, Million J. Stock assessment of yellowfin tuna in the Indian Ocean using MULTIFAN-CL (IOTC-2012-WPTT14-38)[R]. 14th Session of the IOTC Working Party on Tropical Tunas, Mauritius, 24-29 October 2012.
|
| [13] |
Ijima H, Sato K, Matsumoto T, et al. Preliminary stock assessment of yellowfin tuna in the Indian Ocean using SS3 (IOTC–2012–WPTT14–39)[R]. 14th Session of the IOTC Working Party on Tropical Tunas, Mauritius, 24-29 October 2012.
|
| [14] |
Nishida T, Kitakado T. Stock assessment of yellowfin tuna (Thunnus albacares) in the Indian Ocean by SCAA (Statistical-Catch-At-Age) (1950-2014) (IOTC-2015-WPTT17-28) [R]. 17th Session of the IOTC Working Party on Tropical Tunas, Montpellier, France, 22-28 October 2015.
|
| [15] |
Carruthers T, McAllister M. Computing prior probability distributions for the intrinsic rate of increase for Atlantic tuna and billfish using demographic methods[J]. ICCAT Collective Volume of Scientific Papers, 2011, 66(5): 2202-2205. |
| [16] |
McAllister M K, Pikitch E K, Babcock E A. Using demographic methods to construct Bayesian priors for the intrinsic rate of increase in the Schaefer model and implications for stock rebuilding[J]. Canadian Journal of Fisheries and Aquatic Sciences, 2001, 58: 1871-1890. DOI:10.1139/f01-114 |
| [17] |
Maravelias C D, Hillary R, Haralabous J, et al. Stochastic bioeconomic modelling of alternative management measures for anchovy in the Mediterranean Sea[J]. ICES Journal of Marine Science, 2010, 67: 1291-1300. DOI:10.1093/icesjms/fsq018 |
| [18] |
Fonteneau A. A working proposal for a Yellowfin growth curve to be used during the 2008 yellowfin stock assessment (IOTC-2008-WPTT-4)[R]. the 10th Session of the IOTC Working Party on Tropical Tunas, Bangkok, Thailand, 23-31 October 2012.
|
| [19] |
Lunn D J, Thomas A, Best N, et al. WinBUGS-a Bayesian modelling framework: Concepts, structure, and extensibility[J]. Statistics and Computing, 2000, 10: 325-337. DOI:10.1023/A:1008929526011 |
| [20] |
Guan W, Zhu J, Xu L. Analyzing population dynamics of Indian Ocean albacore (Thunnus alalunga) using Bayesian biomass dynamics model (IOTC-2014-WPTmT05-21)[R]. 5th Working Party on Temperate Tunas, Indian Ocean Tuna Commission, Busan, Republic of Korea, 28-31 July 2014.
|
| [21] |
Kéry M. Introduction to WinBUGS for ecologists: A Bayesian approach to regression, ANOVA, mixed models and related analyses[M]. San Diego: Academic Press, 2010.
|
| [22] |
Spiegelhalter D J, Best N G, Carlin B P, et al. Bayesian measures of model complexity and fit (with discussion)[J]. Journal of the Royal Statistical Society-Series B, 2002, 64: 583-639. DOI:10.1111/rssb.2002.64.issue-4 |
| [23] |
Maunder M N. Is it time to discard the Schaefer model from the stock assessment scientist's toolbox?[J]. Fisheries Research, 2003, 61(1-3): 145-149. DOI:10.1016/S0165-7836(02)00273-4 |
| [24] |
Wang S P, Maunder M N, Aires-da-Silva A. Selectivity's distortion of the production function and its influence on management advice from surplus production models[J]. Fisheries Research, 2014, 158: 181-193. DOI:10.1016/j.fishres.2014.01.017 |
| [25] |
Magnusson A, Hilborn R. What makes fisheries data informative?[J]. Fish and Fisheries, 2007, 8: 337-358. DOI:10.1111/faf.2007.8.issue-4 |
| [26] |
National Research Council (NRC). Sustaining Marine Fisheries[M]. Washington DC: National Academy Press, 1998.
|
| [27] |
Babcock E A. Application of a Bayesian surplus production model to preliminary data for south Atlantic albacore[J]. ICCAT Collective Volume of Scientific Papers, 2014, 73(3): 1326-1334. |
| [28] |
Matsumoto T, Nishida T, Kitakado T. Stock and risk assessments of albacore in the Indian Ocean based on ASPIC (IOTC-2014-WPTmT05-22)[R]. 5th Working Party on Temperate Tunas, Indian Ocean Tuna Commission, Busan, Republic of Korea, 28-31 July 2014.
|
| [29] |
Jiao Y, Cortés E, Andrews K, et al. Poor-data and data-poor species stock assessment using a Bayesian hierarchical approach[J]. Ecological Applications, 2011, 21(7): 2691-2708. DOI:10.1890/10-0526.1 |
| [30] |
Hilborn R, Walters C J. Quantitative Fisheries Stock Assessment: Choice Dynamics and Uncertainty[M]. London: Chapman & Hall, 1992.
|
| [31] |
Márquez-Farías J F, Rosales-Juárez F J. Intrinsic rebound potential of the endangered (Totoaba macdonaldi) population, endemic to the Gulf of California, México[J]. Fisheries Research, 2013, 147: 150-153. DOI:10.1016/j.fishres.2013.05.009 |
| [32] |
Prager M. A suite of extensions to a nonequilibrium surplus-production model[J]. Fishery Bulletin, 1994, 92: 374-389. |
| [33] |
Punt A E, Hurtado-Ferro F, Whitten A R. Model selection for selectivity in fisheries stock assessments[J]. Fisheries Research, 2014, 158: 124-134. DOI:10.1016/j.fishres.2013.06.003 |
 2018, Vol. 25
2018, Vol. 25

